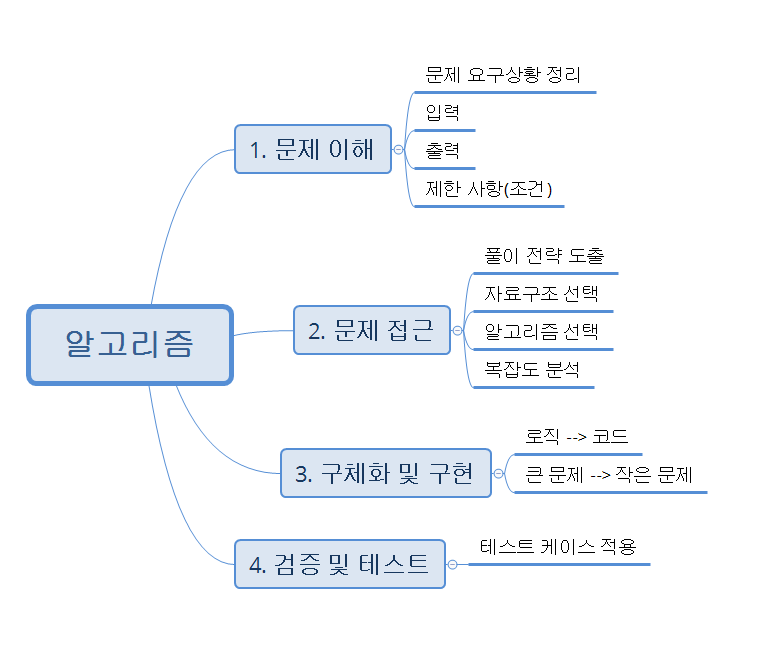
알고리즘 문제를 해결하는 과정에서 중요한 것은 단순히 코드를 작성하는 것이 아니라, 문제를 정확히 이해하고, 그에 맞는 접근 방법을 선택한 후, 구현과 테스트를 통해 해결책을 도출하는 것입니다. 오늘은 백준 10810번 문제, 즉 “공넣기” 문제를 예를 들어 문제 해결을 위한 각 단계가 어떻게 적용되는지 설명해 보겠습니다.
1. 문제 이해
문제 분석
백준 10810번 문제는 도현이가 N개의 바구니에 공을 넣으려는 상황에서, 주어진 구간에 공을 넣는 문제입니다. 각 바구니에는 공을 하나씩만 넣을 수 있고, 공을 넣을 때마다 기존에 들어있던 공은 덮어쓰게 됩니다.
문제의 핵심은 주어진 구간 범위에 대해 공을 넣는 것입니다. 여러 번의 작업을 수행한 후, 각 바구니에 들어있는 공의 번호를 구하는 것이 목표입니다.
문제의 요구사항 정리
이 문제에서 중요한 부분은 구간 처리입니다. 즉, 연속된 범위에 대해 값을 갱신해야 하므로 배열을 사용하여 각 바구니의 상태를 관리하는 방식이 적합합니다.
입력과 출력
- 입력:
N,M, 그리고M개의 공 넣기 작업이 주어집니다. - 출력: 각 바구니에 들어 있는 공의 번호를 출력합니다.
이제 이 문제의 핵심을 명확히 파악한 후, 해결 방법을 고민해야 합니다.
2. 문제 접근
풀이 전략 도출
이 문제를 풀기 위해서 배열을 사용하여 바구니 상태를 추적하는 방식이 적합합니다. 배열의 크기는 N이고, 각 공 넣기 작업을 처리할 때마다 지정된 범위에 값을 갱신하면 됩니다.
자료구조 & 알고리즘 선택
- 배열 사용: 바구니의 상태를 배열로 관리하고, 각 구간에 대해 반복문을 사용해 값을 갱신합니다.
- 반복문: 각 공 넣기 작업에서 지정된 범위(i부터 j까지)에 대해 반복문을 돌며 공을 넣습니다.
구체적인 해결 전략
- 배열 초기화: 바구니는 0으로 초기화하고, 공을 넣을 때마다 구간을 갱신합니다.
- 작업 처리: M번의 공 넣기 작업을 순차적으로 처리합니다.
- 결과 출력: 작업이 모두 끝난 후, 각 바구니에 들어있는 공의 번호를 출력합니다.
이러한 방식으로 문제를 풀면, 시간 복잡도는 O(N * M)으로 충분히 해결 가능합니다. N과 M이 최대 100이므로 이 접근법은 성능에 문제가 없습니다.
3. 구체화 및 구현
코드 구현
이제 문제를 해결하기 위한 구체적인 코드를 작성합니다.
# 입력 받기
N, M = map(int, input().split())
# 바구니 배열 초기화
baskets = [0] * N # N개의 바구니, 초기값은 모두 0
# M번의 공 넣기 작업 처리
for _ in range(M):
i, j, k = map(int, input().split())
# i~j 구간에 번호 k 공을 넣기 (배열은 0부터 시작하므로, i-1부터 j-1까지 갱신)
for x in range(i-1, j):
baskets[x] = k
# 결과 출력
print(' '.join(map(str, baskets)))
코드 설명
- 배열 초기화:
baskets = [0] * N을 통해 바구니의 초기 상태를 모두 0으로 설정합니다. - 작업 수행: M번의 공 넣기 작업을 처리합니다. 각 작업에서 지정된 구간(i부터 j까지)만큼 반복하며 해당 범위의 바구니에 공 번호를 넣습니다.
- 결과 출력:
print(' '.join(map(str, baskets)))를 사용해 바구니에 들어있는 공의 번호를 출력합니다.
이 코드는 각 작업을 순차적으로 처리하고, 배열을 이용해 구간을 갱신하는 방식으로 문제를 해결합니다.
4. 검증 및 테스트
예제 입력 1
입력: 5 4 1 2 3 3 4 4 1 4 1 2 2 2
출력: 1 2 1 1 0
설명:
- 첫 번째 작업: 1번과 2번 바구니에 3번 공을 넣습니다 →
[3, 3, 0, 0, 0] - 두 번째 작업: 3번과 4번 바구니에 4번 공을 넣습니다 →
[3, 3, 4, 4, 0] - 세 번째 작업: 1번부터 4번 바구니에 1번 공을 넣습니다 →
[1, 1, 1, 1, 0] - 네 번째 작업: 2번 바구니에 2번 공을 넣습니다 →
[1, 2, 1, 1, 0]
예제 입력 2
입력: 3 2 1 3 2 2 3 1
출력: 2 1 1
설명:
- 첫 번째 작업: 1번부터 3번 바구니에 2번 공을 넣습니다 →
[2, 2, 2] - 두 번째 작업: 2번과 3번 바구니에 1번 공을 넣습니다 →
[2, 1, 1]
극단적 경계값 검증
- 최댓값 테스트:
N=100과M=100인 경우에도 코드가 잘 동작합니다. 각 작업에서 구간을 갱신하는 방식은 시간 복잡도O(N * M)로 처리할 수 있어 성능에 문제가 없습니다.