알고리즘을 공부하다 보면 스택(Stack)과 큐(Queue)는 필수적으로 이해해야 하는 개념입니다. 이 글에서는 자바와 파이썬에서의 구현 차이점을 비교하고, 스택과 큐를 활용한 백준 17298번 오큰수 문제에 적용해서 설명하겠습니다.

1. 스택(Stack)

1.1 개념

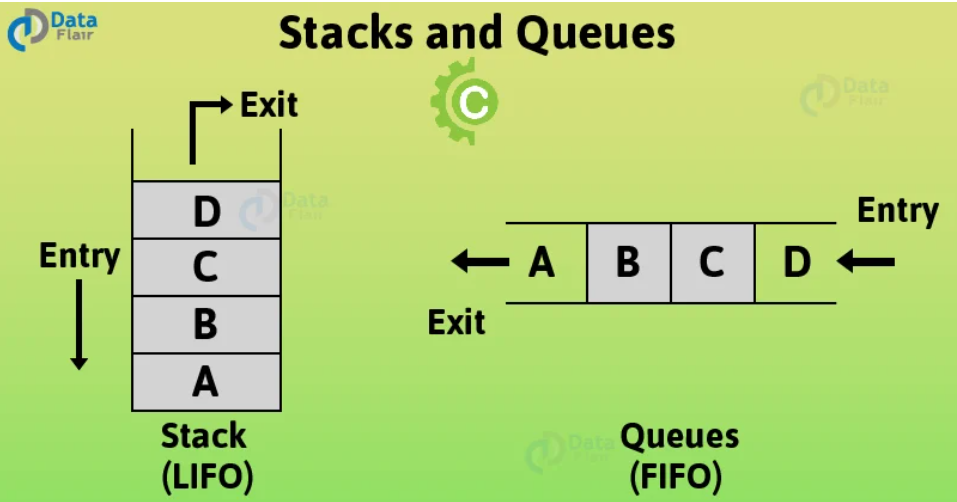
스택(Stack)은 후입선출(LIFO, Last In First Out) 구조를 가지는 자료구조입니다. 즉, 마지막에 삽입된 데이터가 가장 먼저 제거됩니다.

1.2 Java와 Python에서의 스택 구현

연산	Java (Stack)	Python (list 활용)
생성	`Stack<Integer> stack = new Stack<>();`	`stack = []`
추가(push)	`stack.push(10);`	`stack.append(10)`
제거(pop)	`stack.pop(); // 마지막 요소 제거`	`stack.pop()`
맨 위 요소 확인(peek)	`stack.peek();`	`stack[-1]`
비어 있는지 확인(isEmpty)	`stack.isEmpty();`	`len(stack) == 0`

Java 코드 예제 (Stack)

import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();
        stack.push(10);
        stack.push(20);
        stack.push(30);
        System.out.println(stack.pop()); // 출력: 30
        System.out.println(stack.peek()); // 출력: 20
        System.out.println(stack.isEmpty()); // 출력: false
    }
}

Python 코드 예제 (Stack)

stack = []
stack.append(10)
stack.append(20)
stack.append(30)
print(stack.pop())  # 출력: 30
print(stack[-1])  # 출력: 20
print(len(stack) == 0)  # 출력: False

2. 큐(Queue)

2.1 개념

큐(Queue)는 선입선출(FIFO, First In First Out) 구조를 가지는 자료구조입니다. 즉, 먼저 들어온 데이터가 가장 먼저 나갑니다.

2.2 Java와 Python에서의 큐 구현

연산	Java (`Queue` 활용)	Python (`collections.deque` 활용)
생성	`Queue<Integer> queue = new LinkedList<>();`	`from collections import deque` `queue = deque()`
추가(enqueue)	`queue.offer(10);`	`queue.append(10)`
제거(dequeue)	`queue.poll(); // 첫 번째 요소 제거`	`queue.popleft()`
맨 앞 요소 확인(peek)	`queue.peek();`	`queue[0]`
비어 있는지 확인(isEmpty)	`queue.isEmpty();`	`len(queue) == 0`

Java 코드 예제 (Queue)

import java.util.LinkedList;
import java.util.Queue;

public class Main {
    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(10);
        queue.offer(20);
        queue.offer(30);
        System.out.println(queue.poll()); // 출력: 10
        System.out.println(queue.peek()); // 출력: 20
        System.out.println(queue.isEmpty()); // 출력: false
    }
}

Python 코드 예제 (Queue)

from collections import deque

queue = deque()
queue.append(10)
queue.append(20)
queue.append(30)
print(queue.popleft())  # 출력: 10
print(queue[0])  # 출력: 20
print(len(queue) == 0)  # 출력: False

3. 백준 17298번 오큰수 문제 해결 (Python)

문제 설명

주어진 수열에서 각 원소의 “오큰수”를 찾는 문제입니다. 오큰수는 자기 오른쪽에 있으면서 가장 왼쪽에 있는 자기보다 큰 수를 의미합니다.

문제 풀이 (Python)

n = int(input()) # 배열의 크기 입력 받기 
a = list(map(int, input().split())) # 수열을 리스트로 입력 받기
myStack = [] # a 리스트의 인덱스를 저장할 stack 선언

# a 하나씩 순회하면서
for i in range(len(a)):
    while myStack and a[myStack[-1]] < a[i]: # myStack이 비어있지 않고 myStack의 top심벌의 인덱스의 a값보다 현재 a[i]이면(오큰수)
        a[myStack.pop()] = a[i] # myStack의 top심벌의 인덱스의 a값을 현재 a[i](오큰수)로 할당
    myStack.append(i) # myStack의 a의 인덱스 값 차곡차곡 저장 ex 0, 1, 2, 3 ...

for i in range(len(myStack)): # myStack에 남아있는 값들은 오큰수가 없는 a의 인덱스들
    a[myStack.pop(0)] = -1 # -1 할당

# 결과 출력
print(*a)

풀이 과정

스택을 활용하여 각 원소의 오큰수를 찾는다.
스택에는 인덱스만 저장하여, 원소 비교 시 활용한다.
현재 원소가 스택의 top보다 크면, 스택에서 인덱스를 꺼내 해당 위치에 현재 원소를 저장한다.
끝까지 비교한 후에도 스택에 남아있는 인덱스들은 오큰수가 없는 경우이므로 -1을 저장한다.
최종 결과를 출력한다.

4. 정리

개념	설명
스택(Stack)	후입선출(LIFO) 구조, DFS/백트래킹에서 활용
큐(Queue)	선입선출(FIFO) 구조, BFS에서 활용
Java에서 스택	`Stack` 클래스를 사용 (`push()`, `pop()`, `peek()`)
Python에서 스택	`list` 활용 (`append()`, `pop()`, `[-1]`으로 맨 위 요소 확인)
Java에서 큐	`Queue` 인터페이스 (`offer()`, `poll()`, `peek()`)
Python에서 큐	`collections.deque` 활용 (`append()`, `popleft()`, `[0]`)

스택과 큐는 알고리즘 문제 해결에서 자주 등장하는 핵심 자료구조입니다. 각각의 개념과 활용법을 익히고, DFS/BFS 같은 탐색 기법에도 응용해보는 경험이 필요합니다.