6. 깊이 우선 탐색(DFS)
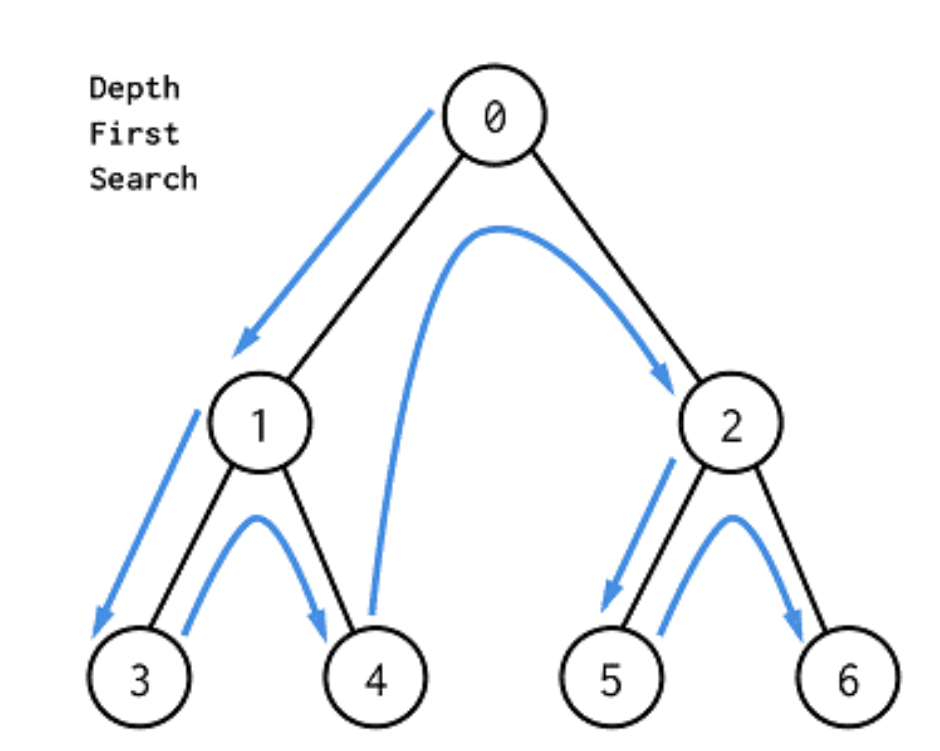
DFS(깊이 우선 탐색)는 그래프의 모든 노드를 탐색하는 기본적인 방법 중 하나로, 스택(Stack)의 원리를 이용합니다. 이번 글에서는 DFS의 개념과 원리를 정리하고, 백준 11724번 “연결 요소의 개수” 문제를 예제로 DFS의 활용법을 살펴보겠습니다.
1. DFS의 구성 요소
DFS를 구현하기 위해 필요한 주요 구성 요소는 다음과 같습니다.
1.1 인접 리스트 (Adjacency List)
그래프는 보통 인접 리스트를 활용하여 구현합니다. 인접 리스트는 그래프의 노드와 간선을 리스트 형태로 표현하는 방식입니다.
- 방향 그래프: 주어진 방향만 고려하여 간선을 저장
- 무방향 그래프: 간선이 양방향이므로, 양쪽 노드 모두에 간선을 저장
1.2 방문 리스트 (Visited List)
그래프의 각 노드 방문 여부를 저장하는 리스트입니다. 방문한 노드는 True로 변경하여 중복 방문을 방지합니다.
1.3 DFS 함수
DFS는 재귀 함수를 사용하여 현재 노드에서 연결된 모든 노드를 탐색합니다.
- 방문하지 않은 노드이면 방문 처리 후, 해당 노드에서 다시 DFS 호출
- 재귀 호출을 통해 깊이 우선 탐색이 진행됨
1.4 노드 개수만큼 DFS 실행
모든 노드를 방문하기 위해 노드 개수만큼 DFS를 실행합니다. DFS가 실행될 때마다 새로운 연결 요소(혹은 경로)가 발견되므로, 연결 요소의 개수를 세는 데 유용합니다.
2. DFS의 구현
import sys
# 재귀 호출 한도를 높임
sys.setrecursionlimit(10000)
# 입력 받기
n, m = map(int, sys.stdin.readline().split())
# 인접 리스트 및 방문 배열 초기화
adj_list = [[] for _ in range(n + 1)]
visited = [False] * (n + 1)
# 그래프 입력 받기
for _ in range(m):
u, v = map(int, sys.stdin.readline().split())
adj_list[u].append(v)
adj_list[v].append(u) # 무방향 그래프이므로 양방향 추가
# DFS 함수 정의
def DFS(node: int):
for neighbor in adj_list[node]:
if not visited[neighbor]:
visited[neighbor] = True
DFS(neighbor)
# DFS 실행 및 연결 요소 개수 세기
count = 0
for i in range(1, n + 1):
if not visited[i]:
visited[i] = True
DFS(i)
count += 1
sys.stdout.write(f"{count}\n")
3. 예제 실행 결과
입력 예제 1
6 5
1 2
2 5
5 1
3 4
4 6
출력 예제 1
2
입력 예제 2
6 8
1 2
2 5
5 1
3 4
4 6
5 4
2 4
2 3
출력 예제 2
1
4. DFS의 동작 원리
DFS는 스택(Stack) 구조를 사용하여 탐색이 이루어집니다.
- 현재 노드를 방문 처리 (
visited[i] = True) - 방문한 노드에서 연결된 모든 노드에 대해 DFS 재귀 호출
- 연결된 모든 노드를 방문하면 재귀 함수가 종료되며 탐색 완료
DFS를 활용하면 연결 요소(Connected Component)를 탐색할 수 있으며, 특정 문제에서는 그래프의 경로 탐색이나 사이클 검출 등에 사용됩니다.
5. 정리
| 구성 요소 | 설명 |
|---|---|
| 인접 리스트 | 그래프를 리스트로 표현하여 간선 정보를 저장 |
| 방문 리스트 | 방문한 노드를 기록하여 중복 방문 방지 |
| DFS 함수 | 재귀를 이용하여 깊이 우선 탐색 수행 |
| 반복문을 통한 DFS 실행 | 그래프의 모든 노드에 대해 DFS를 실행하여 연결 요소 개수 탐색 |