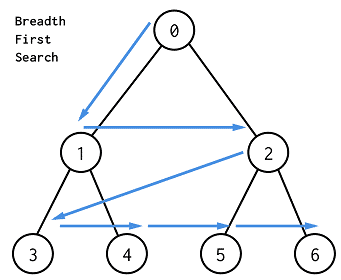
BFS는 그래프 탐색에서 최단 경로를 찾거나 연결된 요소를 탐색하는 데 유용한 알고리즘입니다. 이 글에서는 BFS의 원리를 설명하고, 백준 2178번 “미로 탐색” 문제를 예로 들어 구현 과정을 정리하겠습니다.

구성요소

BFS를 구현하기 위해 필요한 주요 구성요소는 다음과 같습니다.

1. 큐 (Queue)

BFS는 선입선출(FIFO, First In First Out) 구조를 이용하므로, 탐색할 노드들을 저장하는 큐(Queue) 가 필요합니다.

2. 방문 리스트

각 노드가 방문되었는지 여부를 저장하는 리스트를 만들어 중복 방문을 방지합니다.

3. 방향 벡터

상하좌우 이동을 쉽게 처리하기 위한 방향 벡터를 사용합니다.

4. BFS 함수 실행

큐에서 노드를 하나씩 꺼내어 탐색하고, 인접한 노드를 다시 큐에 넣어주는 과정으로 진행됩니다.

구조

from collections import deque
import sys

# 입력 받기
n, m = map(int, sys.stdin.readline().split())

miro = []
visited = [[False] * m for _ in range(n)]
for i in range(n):
    miro.append(list(map(int, sys.stdin.readline().strip())))  # 사용자 입력 받기

# 방향 벡터 (상, 하, 좌, 우)
dy = (-1, 1, 0, 0)
dx = (0, 0, -1, 1)

# BFS 함수 정의
def BFS(y: int, x: int):
    queue = deque()
    miro[y][x] = 1  # 루트 노드의 값(길이)를 1로 설정
    queue.append((y, x))  # 시작점 추가
    visited[y][x] = True  # 시작점 방문 처리

    while queue:
        y, x = queue.popleft()  # 현재 위치

        for i in range(4):  # 상하좌우 탐색
            ny = y + dy[i]
            nx = x + dx[i]

            # 미로 범위를 벗어나지 않고, 이동 가능한 곳인지 확인
            if 0 <= ny < n and 0 <= nx < m and not visited[ny][nx] and miro[ny][nx] == 1:
                visited[ny][nx] = True  # 방문 처리
                miro[ny][nx] = miro[y][x] + 1  # 최단 거리 갱신
                queue.append((ny, nx))  # 큐에 추가

    return miro[n - 1][m - 1]  # 최종 거리 반환

# 결과 출력
print(BFS(0, 0))

실행 예시

입력
```
4 6
101111
101010
101011
111011
```
출력
```
15
```

BFS 동작 원리

시작점 (0,0)에서 탐색 시작: (0,0)을 큐에 넣고 방문 표시
상하좌우 이동하며 탐색: 이동할 수 있는 방향으로 계속 확장
최단 거리 업데이트: 각 위치에 도달할 때의 이동 횟수를 저장
도착점 (n-1, m-1)에 도달하면 종료

정리

BFS 구성요소	설명
큐(Queue)	노드를 방문할 순서를 저장하는 자료구조 (FIFO)
방문 리스트	중복 방문을 방지하기 위한 리스트
방향 벡터	상하좌우 이동을 쉽게 처리하기 위한 벡터
최단 거리 갱신	이동할 때마다 현재 거리 +1을 저장하여 최단 경로 탐색

BFS는 최단 경로를 찾는 데 매우 유용한 탐색 알고리즘으로, 미로 탐색뿐만 아니라 그래프 탐색, 네트워크 분석, 길 찾기 등 다양한 분야에서 활용됩니다.